| |
Contents | EBJ Home | Single molecule measurements and biological motors |
a)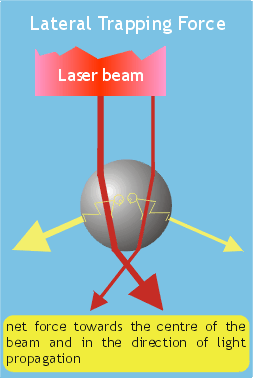 |
b)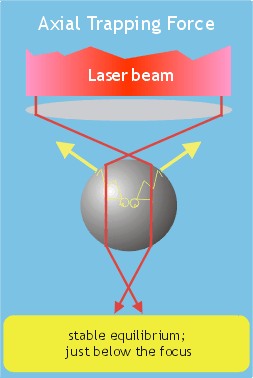 |
| Ray optics model
of optical tweezers shows how optical forces are generated as light
momentum is transferred to the electrons of a dielectric particle ("stick-man"
cartoons). a) shows that a laser beam of Gaussian intensity profile will draw a particle to the centre of the beam and propel it in the direction of light propagation. b) shows how a tightly focused laser beam can produce forces that act against the direction of light propagation - producing a three-dimensional trap. The dielectric particles must be of higher refractive index than the bathing medium and should be of similar size to the diffraction-limited spot diameter (Svoboda & Block 1994). |
|
A detailed analysis of the physics of optical trapping is beyond the scope of this article; see the diagrams above for a simple ray-optics explanation. The theory of trapping is reviewed in more detail by Svoboda and Block (1994) and Ashkin (1992). Although there is a body of theory describing the trapping forces, in most cases it is necessary to make empirical measurements of trap stiffness. The theory is a useful guide in designing and optimising apparatus, and should give a close approximation to what is practically achievable. For this reason we present a potted summary here; refer to the cited sources for further details.
The theory has severe limitations in describing real-world trapping applications. For example, it is really only useful for transparent spherical objects (although in fact most of the “handles” used by researchers meet this criterion). The best theories are for the Mie (d>>λ) and Rayleigh (d<<λ) regimes; but in typical applications d≈λ (for example, using a 1 μm bead in a trap produced by a Nd:YAG laser, λ = 1.064 μm).
The optical forces experienced by a particle in an optical trap can usefully be divided into the gradient force and the scattering force. The scattering force is present even in the absence of a stable trap, and tends to push objects along the beam in the direction of propagation. The gradient force pushes objects towards the highest light intensity, and is responsible for optical trapping. A trap is produced when the gradient force on the beam axis is stronger than the scattering force. The bead is then stably trapped at a position slightly beyond the focal point of the beam. In general, a trap's stiffness in the axial (z) direction is rather lower than in the x and y directions. However, most experimental work relies mainly on the bead's motion in the x or y directions.
To achieve the tight focus required for trapping, a high numerical aperture objective lens is used. This allows the beam to be focussed to a diffraction limited spot, and also allows highly converging rays at the focus, which are important for stable axial trapping. The laser beam usually has a Gaussian (TEM00) profile, in which case it should slightly overfill the back aperture of the objective (Ashkin, 1992).
Optical tweezers have the useful property that the restoring force is linearly proportional to displacement (at least over positions near to zero). This linearity means that the strength of the trap can be represented simply by a stiffness value. To put it another way, the trap is analogous to a simple spring i.e., it obeys Hooke's law. Most of the theory described below relies on this property of optical traps. At greater displacements, as one would expect, this linearity breaks down and eventually the bead can escape from the trap. The escape force required to do this was previously widely used as a parameter to describe an optical trap, but has limited usefulness, as it is difficult to measure accurately and most experimental work is, in any case, done in the linear part of the trap.
This linear or Hookean behaviour is one of the most useful properties of optical tweezers. As well as providing an obvious way of measuring very small forces, is simplifies the mathematical properties of the system, as described below. The behaviour of a bead in an optical trap can then be described in a relatively simple manner, as is discussed in the following sections.
| Contents | Next |