|
|
Contents | EBJ Home | Single molecule measurements and biological motors |
For any application where it is necessary to measure forces on, or displacements of, objects in the optical trap, some kind of position detector will need to be used. For example, this is necessary to measure the properties of molecular motors, to calibrate trap stiffness, or to provide feedback. Since nanometre precision is required, the signal to noise ratio becomes an important issue. There are several sources of noise which may come into play; different sensing methods suffer from these noise sources to different extents.
The most intuitive detection methods simply use the image of the trapped bead. These methods use conventional bright field, phase or DIC microscopy to produce an image that is cast onto an electronic detector. The output of this detector is then processed in some way to produce a position signal in one or two dimensions. The chief difference between methods lies in the type of detector used. This can be a “scanning” type of sensor such as a CCD in which pixels or image elements are accessed sequentially; or it may be a multi-segment or position-sensitive photodiode type of sensor where a continuous analogue signal is produced. The latter type of detector generally provides higher bandwidth. A compromise type of detector could be the linear array type of CCD or photodiode which might be ideal for multiple bead applications.
One of the chief difficulties with imaging approaches is the low contrast which is generated by the object, typically a transparent sphere in water.
Video images can be used, by a method involving cross-correlation and centroid calculation (Gelles et al., 1988), but this method has inherent limitations. Although the resolution is surprisingly good (1-2 nm) – significantly better than the theoretical resolution of the light microscope (Rayleigh criterion) or the pixel size of most cameras – it is not as good as can be achieved by other methods. A more severe limitation is the time resolution. The frame rate of standard video is 25 Hz (CCIR) or 30 Hz (NTSC); this is a factor of 10 lower than the roll-off frequency of Brownian motion under typical conditions. Another problem is that a significant amount of computing power is needed for the cross-correlation and centroid calculations, making it difficult to do real time detection. This, coupled with other problems such as video noise and frame interlace, make this approach impractical for most studies. (Although some of these problems can be circumvented using non-standard video hardware – e.g. higher frame rates, progressive scan, etc.)
Quadrant photodiode detectors (see below) provide many advantages over video for position sensing. As compared to the video method, they offer much higher bandwidth, giving sub-millisecond time resolution. They can also give higher spatial resolution. When used in an imaging method, the image of the trapped bead is projected onto the detector in the same way as a camera. This means that the detector can simply be mounted onto the camera port of a microscope. However, in the imaging method, the trapped bead must be aligned with the detector. To facilitate this, a detector would typically be mounted on an x-y translator. This method is readily compatible with multiple traps, simply requiring separate detectors for each trapped object. This method gives both x and y signals, and because the position is measured relative to the detector (not the trap), this method is easy to calibrate and suitable for position clamp feedback. The limiting factor with this method is usually the shot noise from the bright field illumination used.
These methods typically use the trapping laser itself as the source of illumination for the position sensor, although in some cases it is possible to use a separate laser for this purpose. In general, where the trapping laser is used, displacements are measured relative to the trap; with a separate laser, they are measured relative to the focal point of that laser. Because of the intensity of the laser light used, these methods tend not to be limited by the shot noise of the illumination. Instead, laser pointing and amplitude stability become the key issues. For a more detailed review of these methods, see (Visscher et al., 1996).
This method was one of the first to be developed (Svoboda et al., 1993; Svoboda and Block, 1994). The trapping laser beam is split into two orthogonal polarisation components by a Wollaston prism (part of standard DIC optics) resulting in two overlapping foci which produce a single trap. The beams are then recombined by a second Wollaston prism and the ellipticity of the light measured. A trapped bead will retard one of the polarisation components more than the other, (unless it is in the centre of the trap), resulting in the light becoming elliptically polarised. This system has a number of advantages; it gives very high resolution and low noise, and excellent time resolution. It is also relatively resistant to vibration, and does not need to be aligned as it measures position relative to the trap. However, the latter aspect means that it is not suitable for feedback applications. It is also limited to measuring in one dimension only. Normally it is only suitable for single trap applications, but it might be possible to modify it for time-sharing applications, in a similar fashion to the next method.
This method also uses the trapping laser light, and shares with the preceding method the advantages of high light intensity and no need for detector alignment. Moreover, it permits measurement in both x and y directions. Its disadvantages are similar, in that because position is measured relative to the trap, calibration and feedback become problematic. The method operates by imaging not the bead, but the condenser back focal plane, onto a quadrant photodiode. The image in the back focal plane is an interference pattern between the trapping laser light and the laser light which has been scattered by the trapped bead (Allersma et al., 1998; Gittes and Schmidt 1998a).
Although the optics are very different for the two quadrant photodiode methods, the detector and electronics are essentially the same, except that a larger photodiode is needed for the BFPI method. This method is applicable to time-sharing optical traps, but it is necessary to “de-multiplex” the position signals of the two traps, as discussed below.
A difficulty with this method is that motion of the trap also generates a residual signal, which can be hard to eliminate. This is not a problem if the trap remains in a fixed position, but where a forcing function is applied to the trap in order to make a measurement or calibrate the trap stiffness or detector sensitivity, some means must be found to circumvent this problem.
By intercepting all of the light passing through a trapped bead, it is possible to directly infer (by conservation of momentum) the forces acting on a trapped particle (Smith et al., 1996). This method’s advantage is that it does not require calibration. However, it is only compatible with the dual-beam trap and does not work with the single beam trap, which severely limits its applications.
A method related to the BFPI method (Ghislain and Webb, 1993; Ghislain et al., 1994) has been used to measure both axial and lateral displacements in the optical trap. Like the BFPI method, this technique uses the trapping light after it has passed through the trapped object, although optically it is rather different. However, as described, it cannot distinguish the direction of movement.
The methods which we will consider in more detail are those based on quadrant photodiodes. These detectors can be used in imaging or non-imaging modes. Although the optics are rather different, the detectors and supporting electronics are very similar (although a larger detector is used for the BFPI method to cover the whole back focal plane image of the condenser).
Quadrant photodiodes are part of a family of position sensitive light detectors. They simply consist of four separate photodiodes, each quadrant shaped, which together make up a circle (see figure). (Square and single axis (i.e. two element) versions are also available, though rarely used in trapping applications.)
Like all photodiodes, they can be used in a photovoltaic or a photoconductive (reversed bias) mode. The photovoltaic mode is widely used because though it has slower frequency response, it is still fast enough for may applications. It is also simpler electronically and there is no dark current, which means less noise and better sensitivity to low light levels. Typically the four photodiodes share a common cathode (which in photovoltaic mode is connected to ground) and have separate anodes.
The output current from each quadrant is converted to a voltage by the first
stage of amplification (a transresistance amplifier). This configuration
gives a linear relationship between the light intensity and output voltage.
This stage is critical for the frequency response and signal to noise ratio
of the detector. It is typically performed in the detector head itself; the
amplified voltage signals can then be transferred via a screened cable to the
analogue electronics which process them into x and y position
signals. Quad op-amps (such as the Burr-Brown 
OPA404)
are ideal for this application as the electronics can then be made very compact.
Power for the amplifiers can be transferred in the same cable as the quadrant
signals.
Careful choice of feedback resistors for the transresistance amplifier is essential to optimise performance. It may also be necessary to add a capacitor across the feedback resistor to prevent the output from oscillating (or “ringing”). The ideal values of these components can in principle be calculated from the desired performance characteristics, but in practice empirical testing is required as factors like stray capacitance can have a significant effect. However, it is worth considering the way in which these components affect the performance of the device:
Gain: The amplifier gain is proportional to RF. V = I·RF, where V is the output voltage and I is the input current from the photodiode.
Noise: The noise due to the feedback resistor is proportional to the square root of RF. VN = √(4kTRFB) where VN is the rms noise voltage, k is Boltzmann’s constant, T is the absolute temperature and B is the bandwidth considered.
Bandwidth: The corner frequency is inversely proportional to RF. fc = 1/(2πRFC).
The optimal configuration will vary depending on the application. For example, in the bright field imaging case, the light level (and contrast) are relatively low, and a high gain is therefore required. In this case an RF value of 30 MΩ might be typical. With sufficiently high gain, the shot noise in the illumination becomes the limiting factor. Of course is it also necessary for the bandwidth to exceed the desired sampling frequency. In the BFPI case, the level of illumination is much higher, so that a much lower gain is required to prevent saturation of the amplifier (even with the use of IR absorbing filters to attenuate the laser beam). A greater bandwidth is also required to accommodate the “chopping” between trap positions – the corner frequency needs to be much greater than the chopping frequency to ensure that the detector signal settles during each interval. In this case we have used resistor values as low as 10 kΩ with a 47 pF capacitor to prevent ringing (predicted fc ≈ 340 kHz; chopping frequency 5-10 kHz).
There are several variants on the circuit for converting the quadrant outputs into x and y position signals; a simple example is given in the figure above. In this example, after pre-amplification, each adjacent pair of quadrant signals is fed to a differential amplifier. These signals then give partial information about motion in the x or y axis. The signals from each axis are then summed by final stage of amplification, giving the x and y position signals. Other arrangements include reversing the order of the differential and summing stages. Also, it may be useful to generate a total intensity signal by summing all of the quadrants; this may be used to normalise the position signals to make them independent of illumination intensity.
In a single trap apparatus, these x and y signals can then be digitised directly; however, in a time-shared trap apparatus it is necessary to separate the signals from each trap. An example of how this can be done is given in the figure below. Here, the timing signal which controls the “chopping” of the trap positions by the AOD is used to synchronise sample and hold chips which are connected to the x and y position signals from the previous circuit. It is then the outputs from these devices that are digitised. Obviously, in this arrangement the “chopping” frequency imposes an upper limit on the sampling frequency that can be used to acquire data.
 |
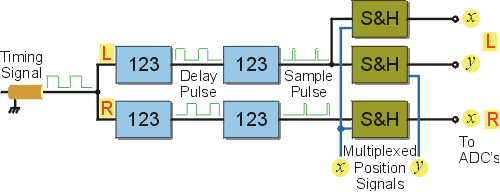| Schematic of circuit for “de-multiplexing”
position signals from time-shared optical traps. The timing signal from
the AOD control circuit is fed to a pair
of monostable multivibrators ( 123),
which produce complementary outputs. The first stage generates a long “delay”
pulse, which allows the AODs to settle.
This is followed by a short “sample” pulse, which is used to
gate the sample and hold chips (S&H) (e.g. LF398N).
In the example shown, there are three sample and hold chips, outputting
the x signals of both traps and the y signal for one of them.
L and R indicate the “left” and “right”
traps respectively. |
|
Previous |
Contents | Next |
