Single molecule measurements and biological motors

Thermal energy

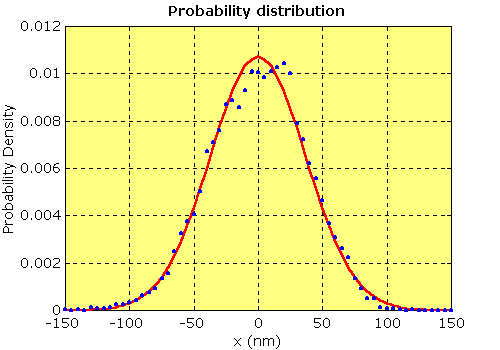Distribution of positions for the record shown previously. The statistical distribution of positions over time is a Gaussian or normal distribution. The width of the distribution is determined by the temperature and the trap stiffness. The red line shows the probability distribution calculated from the trap stiffness. The blue dots show the actual distribution of positions as a histogram with bins 5 nm wide.

The mean thermal energy of an object is kT/2 per degree of freedom, where k is Boltzmann's constant (1.4×10^-23 J·K^-1), and T is the absolute temperature. At room temperature, kT ≈ 4 pN·nm (1 pN·nm = 1 zeptojoule or 10^-21 J). However, the actual distribution of energy is exponential:

P = e^-E/kT

(Boltzmann's law). This, together with the parabolic potential well, means that the distribution of positions over time tends to follow a Gaussian or normal distribution. Thus, if we observe a trapped object for long enough and record its position, then if we plot a histogram of positions it forms a Gaussian shape with a width determined by the temperature and trap stiffness (see figure above). In fact, the variance of the position signal is given by kT/k. In other words, if we know the temperature, we can use the variance as a measure of stiffness (see figure below). Furthermore, if we monitor the variance over time, we can detect changes in stiffness, e.g. when myosin binds to actin.

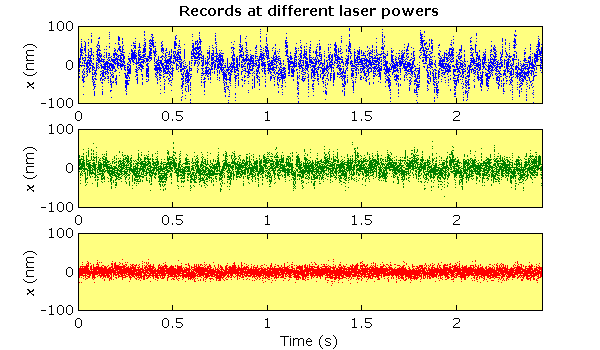Thermal motion varies with trap stiffness. A 1 μm diameter polystyrene sphere was held in an optical trap and its position recorded with a quadrant photodiode at 5 kHz. In successive records the laser diode current was increased (8.72 A, 9.83 A and 14.95 A respectively). With increasing laser power, the trap stiffness increases and the variance of the bead position decreases. The variance can be used to estimate the trap stiffness; the calculated values are 0.0042, 0.0129 and 0.0544 pN·nm^-1 respectively. The trap stiffness may also be estimated from the power spectrum.

Contents