Single molecule measurements and biological motors

Actomyosin trapping

Schematic of an actomyosin trapping experiment. The actin filament (yellow) is suspended between two latex beads in dual optical traps (pink). The filament is brought in proximity to a third bead with attached myosin molecules (mauve). The interactions between actin and myosin are monitored through the bead positions (red arrows).

Myosins are non-processive or weakly processive motors. This has implications both for the way in which experiments are performed, and for the interpretation of the resulting data. Similar considerations will apply to other non-processive motors, or transient intermolecular interactions. We also briefly discuss processive motors.

The “three bead” trapping technique

Because the myosin typically remains bound to the actin filament for a short period of time, it will diffuse away rapidly unless it is held in close proximity. For this reason, in most trapping experiments with myosins, two trapped beads are used, with an actin filament extended between them (see figure).

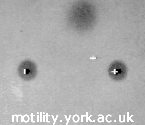
These “bead pairs” or dumbbells are assembled from a fluorescent actin filament and two beads coated with an actin binding protein. As for motility assays, the fluorescent label is usually rhodamine phalloidin. For the actin binding protein, we usually use the HMM fragment of myosin, treated with NEM (N-ethyl maleimide), which binds irreversibly to the actin filament. Other possibilities include gelsolin. A filament is “captured” from solution using the trapped beads (see video).



A pair of fluorescent 1 μm polystyrene beads with a rhodamine–phalloidin labelled actin filament suspended between them, visualised by epifluorescence microscopy.

The flow cells in which trapping experiments are performed are similar to those used in motility assays, except in two significant respects. Firstly, the myosin concentration required to observe individual interaction events is much lower than for sliding motility. Secondly, “pedestals” are needed to raise the myosin above the surface. This is because the trapped beads are typically 1 μm in diameter, and need to be separated from the cover slip surface, so that the actin filament will be a μm or more above the surface. For pedestals we typically use 1.7 μm diameter silica beads. The whole surface, including the beads, is coated in nitrocellulose, which is also what sticks the beads to the cover slip.



Bright field view of an actin-bead assembly interacting with a myosin coated “pedestal”.

The next video shows how the assembled “bead pair” is offered up to the myosin coated “pedestal”. (The actin filament is not visible in bright field). The smaller dark circles are the two trapped beads; the larger one is the surface “pedestal”, coated in this case with rabbit skeletal myosin. The positions of the traps, and of the stage, are shown by computer generated cursors. The video shows the following:

The piezoelectric stage is moved to bring the myosin coated bead close to the actin filament.
As the actin and myosin interact, the right bead is pulled vigorously inwards. The extent of the motion implies that multiple molecules are involved (a lower surface density of myosin would be needed to record single interactions). Since skeletal myosin moves towards the barbed end of actin filaments, this implies that the barbed end is on the right.
The surface bead is moved away and the “bead pair” is rotated through 180°
Now, as expected, the left-hand bead is pulled inwards.
The trapped beads are moved apart so that the assembly is under tension. This is the normal experimental configuration.
Now both beads can be seen to move together (to the right). Periodically the filament “slips” back to the left as the myosins detach.

This illustrates the principle of making single molecule recordings. The surface density used in practice would be lower, and the bead positions would be recorded using some form of position sensor.

Theoretical aspects and data interpretation

Compliances in the “three bead” trapping geometry. The stiffnesses shown dominate the observed compliance in trapping experiments. They are:

κ_trap The trap stiffness

κ_xb The myosin cross-bridge stiffness

κ_con The actin to bead connection stiffness

The stiffness experienced by a trapped bead in this arrangement depends on whether the motor or other protein is bound to the cytoskeletal filament. In the detached state, the stiffness in the x direction, i.e. along the filament axis, is simply twice the trap stiffness, κ_trap. Since the stiffnesses of the actin filament itself, and of the filament-bead linkages, are typically much higher, they do not significantly affect the behaviour of the system.

On the other hand, once the motor is bound to the actin, typically the stiffness becomes a composite of the trap, motor and connection stiffnesses. The filament stiffness is much higher and still does not play a role.

The connection stiffnesses, κ_con, are of the same order as the motor stiffness, κ_xb. Because these stiffnesses are in series with the motor stiffness, this makes it difficult to obtain accurate measurements of motor stiffness and force. This is known as the series compliance problem, and several elaborations of trapping methodology have been developed to overcome it:

If the goal of the experiment is to detect interactions between actin and myosin, then this is possible in normal free-run mode (see below) provided that the connection stiffness is reasonably high. Time resolution is limited by the roll-off frequency of the thermal noise.
If higher time resolution is required, a high frequency, small amplitude sinusoid can be applied to one of the trap positions, and the motion at the other trap monitored (see Veigel et al., 1999). This method gives time resolutions of ~1 ms.
For more accurate stiffness measurements, a low frequency, high amplitude sinusoid can be used. The sinusoid is applied to one bead. The amplitude at the driving bead gives the force applied to the crossbridge, and at the passive bead, the resulting displacement, allowing the stiffness to be calculated (Veigel et al., 1998).
To characterise the behaviour of the motor under known forces, a “force clamp” can be used. This is a feedback arrangement which keeps the force, and thereby the extension of the series compliance, constant (Visscher and Block, 1998).

Detecting interactions

Most actomyosin experiments are done in free-running or displacement mode, where no forcing functions are applied. The challenge then becomes to detect the interaction events in these records. We have recently reviewed the current methods for analysing optical tweezers data (Knight et al., 2001), so we shall present only a brief summary of the problem, and various solutions, here.

The Questions

The information we would like to extract from interaction events includes:

What displacement does the myosin produce?
What are the kinetics (i.e. durations) of the events?
What is the time course of displacement during the events?

The displacement can be obtained from the mean displacement of a large set of events. The kinetics of the rate-limiting step(s) for myosin dissociation (usually ATP binding) can be obtained from an exponential fit to the event lifetimes. By averaging many events together, we can learn about the rise time of displacement, or sub-steps or other processes occurring during the events.

For all of these, particularly 2 and 3 above, it is essential to be able to determine the start and end points of events with good time resolution.

The Problem

When myosin binds to actin, there are two separate effects which can be seen in a displacement record:

The actin filament is displaced from the position it occupied at the moment of binding. Due to the rapid thermal motion of the filament, this starting position is unknown. This means that many events must be averaged to measure the power stroke of the myosin. Furthermore, the displacement is not useful for detecting events as they are likely to lie within the range of thermal motion. This is because the work done is of the order of kT, thermal energy.
The system stiffness is increased by the addition of the myosin and connection stiffnesses. This means that the variance of the thermal motion will fall. This is useful for detecting events, provided that the motor and connection stiffnesses are sufficiently high. However using the variance of thermal noise has two principal limitations for detecting events:
1. Time Resolution. Because the roll-off frequency of the power spectrum of the thermal noise is usually a few hundred Hertz, this limits the time resolution of this method to typically a few tens of milliseconds.
2. Stochasticity. The variance of thermal motion is a statistical measurement of a random process. It is therefore inherently prone to statistical error.
Some non-variance based methods for using the change in stiffness to detect interactions exist; for example the correlation method or the use of high frequency sinusoids.

These effects are illustrated by the trap simulation applet on the next page.

Some Solutions

A wide range of methods have been used to analyse optical tweezers data of non-processive motors. Here is a brief summary (see our review for more details).

Manual Inspection was the method originally used by most workers, but is not considered acceptable today because of problems in consistently identifying events within the range of thermal motion. Automated analysis is more reliable, consistent and objective.
Correlation was the method proposed by Mehta et al. in 1997. This uses the correlation coefficient between the position signals recorded from the two beads. If the filament is under tension, the motions of the beads will be correlated. When myosin binds, the correlation coefficient will drop. This method works well, but in our hands at least the variance based methods give clearer signals.
Variance methods use the drop in amplitude of the thermal noise to identify events. There are several variations:
1. Mean-Variance analysis this method does not attempt to localise events in the record, but rather to derive the myosin working stroke from the record as a whole. We feel that methods which identify the start and finish of events are more widely applicable.
2. Variance Threshold the variance of a running window is calculated, filtered, and a threshold is imposed to detect events. This method works well in practice, but we prefer:
3. Page's Test is a more robust, consistent and precise method of identifying the start and endpoints of events. This is the method we currently favour
4. Hidden-Markov Methods were used in a recent paper by Smith et al. (2001). We have not evaluated this method, but it looks promising.

Processive motors

Most of the myosins that have been studied using optical tweezers are non-processive; in contrast, most kinesins are processive. Recently, myosin V was shown to be processive (Mehta et al., 1999; Veigel et al., In Press), and some non-processive kinesins have been identified.

Processive interactions in the optical tweezers appear as a displacement “staircase”, with sequential displacement events. The starting position for the steps in such a staircase is known, and therefore the power stroke can be obtained directly. The first step, however, is subject to the same uncertainty as non-processive motors.

Because of the large displacements produced by processive motors, the restoring forces can become quite large and will affect the rate of any load-sensitive steps in the motor's kinetic cycle. Ultimately, the motor will stall. Alternatively, a “force clamp” feedback mechanism can be used to track the motor over long distances and under different loads.

Contents